Modeling Bank Reserve Requirement:
This example shows how a few electrical components can be used to model
the reserve requirements of a bank. We use current flow to
simulate money flowing into and out of the bank as well as
Standard Simulation Conditions.
This model is shown below. The capacitor C1 holds the bank assets and C2 keeps track
of the required reserve. If the voltage (or money) on C1 ever becomes less than the voltage on C2,
then the bank is not meeting its reserve requirement. The Initial Condition (I.C.) component is
used to set the voltage on these capacitors to zero at the start of this particular simulation.
The deposits and withdraws subject to the reserve requirement are added to C1 by way of
resistor R1.
Deposits will flow through R1 from circuit node 3 (in_out label) to node 1. Withdraws
will result in current flow in the opposite direction (node 1 to node 3).

R1 will sense
the amount of flow into, or out of, C1 and present a proportional voltage at the Equation
Controlled Current Source (ECCS) Y input. This ECCS adds or removes the required reserve
assets at C2. The percent reserve requirement is presented at the ECCS X input. The
current in the ECCS obeys the equation Y*X/100. Note that the X is divided by 100 to
convert the reserve percentage into a fraction and then multiplied by deposit or withdraw amount
at the Y input. For deposits, the ECCS adds charge to C2. For a withdraw, the voltage
at the Y input becomes negative causing the ECCS to reverse the direction of its current
flow and remove charge (money in this case) at C2.
The SPICE description of this model is shown below.
R.R1 1 3 1.0
B.Ifunc1 0 2 I=(v(3)-v(1))*(v(4)-v(0))/100
C.C2 2 0 1.0
C.C1 1 0 1.0
.IC v(1)=0 v(2)=0
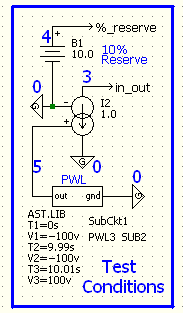
The circuit shown at the left provides test conditions to check the performance
of this model. In this example, the battery, B1, sets the reserve requirement at a fixed 10%.
The Voltage Controlled Current Source, I2, provides deposits and withdraws. It is controlled
by the PWL
component shown at the bottom. The PWL provides $100K per month of deposits for the
first 10 months.
At 10 months into the simulation, the PWL will stop deposits and then make withdraws at
$100K per month for the next 10 months.
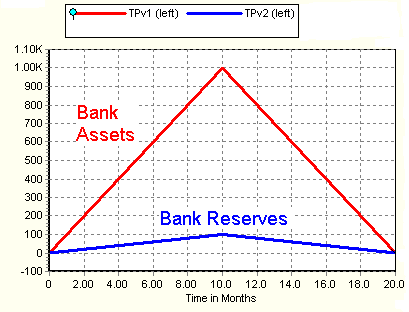
The simulation result is shown below. Since no loans or other activities
are done by the bank during this time, the reserves should always be 10%
of the assets.
Back


